[Python] 분수 덧셈 문제풀이

분수 덧셈 문제풀이

문제

첫 번째 분수의 분자와 분모를 뜻하는 numer1, denom1, 두 번째 분수의 분자와 분모를 뜻하는 numer2, denom2가 매개변수로 주어집니다. 두 분수를 더한 값을 기약 분수로 나타냈을 때 분자와 분모를 순서대로 담은 배열을 return 하도록 solution 함수를 완성해보세요.

 

제한사항

0 <numer1, denom1, numer2, denom2 < 1,000

 

입출력 예

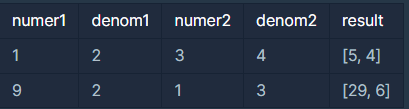
풀이

두 분모 (denom) 이 서로 나눌 수 없는 수 (소수) 인 경우에 기본적인 분수의 덧셈은 다음과 같다.

numer1 / denom1 + numer2 / denom2 = (numer1 * denom2 + numer2 * denom1) / denom1 * denom2

즉, 쉬운 표시로는 a/b + c/d = (a*d + b*c) / b*d 이다. 

여기에 두 분모가 서로 나눌 수 있을 때를 대비하여 최대공약수(gcd)를 이용해주면 된다.

위와 같이 각각 구해서 나온 분자(numer) 와 분모(denom) 에 각각 최대공약수로 나눈 몫을 구하면 된다.

 

예를 들어, 입출력 예 1번을 보면 1/2 + 3/4 =(1*4 + 2*6) / 2*4 인데, 2는 4의 약수이다.

수학적인 계산으로만 보았을 때, 1/2 에만 분자, 분모 각각 2를 곱해주면 되는 일이다.

이를 각각 곱하고 더한 분자와 분모의 최대공약수를 이용하는 것이다.

구현

• math 함수 이용

import math
def solution(numer1, denom1, numer2, denom2):
    numer = numer1*denom2 + numer2 * denom1
    denom = denom1 * denom2
    gcd = math.gcd(denom, numer)
    return [nummer//gcd, denom//gcd]

• 유클리드 호제법을 써서 최대공약수(gcd) 구하는 함수 구현

def gcd(a,b):
	while b>0:
    	a, b = b, a%b
    return a

def solution(numer1, denom1, numer2, denom2):
    numer = numer1*denom2 + numer2 * denom1
    denom = denom1 * denom2
    gcd = gcd(denom, numer)
    return [numer//gcd, denom//gcd]

 

[참고] : 유클리드 호제법

https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95